我们知道，高数中求解极限的方法是多种多样的，这就使得考查极限运算的灵活性增大。但是每种方法都有各自的适用范围，单调有界收敛准则也不例外。
关于该单调有界性，我们可以这么看，如是单调增函数，需要满足有上界，这样该数列则是极限存在的，否则将无限增大;同样地道理，对于单调减的函数，需要满足有下界，否则数列将无限减小。
在证明的过程中，考生应首先证明有界性，之后再证明单调性，否则，讨论单调性时，可能存在函数在不同的区间上单调性不同的问题，这样就需要分类讨论。而先证明有界性，实质上就缩小了讨论单调性的区间和范围，有助于帮助考生确定单调性。
在考试中，考生可以先在草稿纸上写写数列的前三四项，帮助我们确定单调性的增减，通常题目中所求的极限的存在的，这时我们可以先对递推关系式两端求极限，解出a的值，确定数列的上界或者下界。下面就可以在答题纸上正式作答了，首先使用数学归纳法证明数列的有界性，其次计算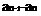
的正负以确定单调性。这样就完成了第一步的证明，下面就设数列的极限为a，对递推关系式两端求极限解出a的值即可。
单调有界收敛准则的使用，是有一定的规则和适用范围的，同时时候的步骤也是较为条例和规范的。考生只要稍加练习，这部分分数是完全可以拿到手的。
【如何使用单调有界收敛准则求解数列极限】相关文章：
