目前,我们已经对导数和微分的基本概念有了一定的了解,特别是导数的定义。通过导数的定义,我们可以计算出每个函数的导数,但其可操作性却太差。所以,我们需要引入求导法则。一切公式从本质上讲都是从导数的定义推出来的,为了便于大家理解和掌握,查字典公务员考研数学辅导老师吴金凤将从基本定义出发推导出所有的公式。
首先,通过可导与可微部分,我们可以得到求导公式:
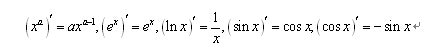
上述公式,我们在可导与可微部分通过导数的定义都直接证明过了。这是我们知道的第一批求导公式。在讲解求导法则的过程中,我们还会对常用的基本求导公式进行补充。首先看下求导法则:
1、导数的四则运算法则
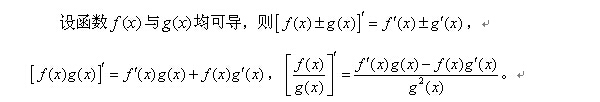
有了导数的四则运算,通过求导公式得到的5个函数相互之间加减乘除的导数就可以计算了。如tanx,cotx,secx,cscx 的导数,这四个函数的求导公式我们也要牢牢记住。
由导数的定义和四则运算,我们能够计算的导数还是非常有限。因为函数不仅仅是通过四则运算组成的。事实上,大多数复杂的函数都存在复合的关系,因此,不解决复合函数求导的问题是没有办法计算更为复杂的函数的导数问题,因此我们还需要复合函数求导法则。
2、复合函数求导法则

对于复合函数求导的链式法则我们只要记住结论就行,其实,该公式的内容可以概括为:要求函数的导数时,先将中间变量看成一个整体 u,先对它求导,再乘以它对最终变量的导数。如果函数有多重复合,逐层求导再相乘即可。由复合函数的求导公式,可以得到 ax的导数公式。
引入了复合函数求导法则之后,我们能处理的函数类型就大大增加了。但现在我们还有一种函数的求导工作无法处理。构成函数的基本运算除了四则运算与复合运算之外,还有反函数。因此,要完整地掌握所有函数的导数计算方法,还需要反函数求导法则。
3、反函数求导法则

以上是查字典公务员考研数学辅导老师吴金凤为大家分析的导数计算部分的三大求导法则,这是计算导数的基础,望大家熟练掌握。同时,通过导数的定义和求导法则得到的十三个基本求导公式我们也要熟记于心。
【中公考研名师详解:高等数学之导数的计算】相关文章: