行测试卷中,数学运算部分是很多考生头疼的题型,经过多年的研究,我发现其实数学运算部分并没有考生们想象的那么难,因为数学运算部分就是那么些题型,每种题型又都有自己的特点和常用解决方法,只要我们弄明白了每种题型,那么数学运算便自然攻克。今天我们来分析一下混合问题。
混合问题是数学运算部分常考的一种题型,常用的知识点为:

浓度=
常用方法为:方程法 利用溶质相等或者浓度相等来构造等量关系
十字交叉法 混合问题的简便计算方法
分析猜答案法 深刻理解混合本质,分析题目猜出答案
我们一起分析一道题目:
甲杯中有浓度17%的溶液400克,乙杯中有浓度为23%的同种溶液600克,现在从甲,乙取出相同质量的溶液,把甲杯取出的倒入乙杯中,把乙杯取出的倒入甲杯中,使甲,乙两杯溶液的浓度相同,问现在两杯溶液浓度是多少?
方程法:
利用浓度相等,我们可以构造方程
设:从甲乙两杯中分别取出x克,则
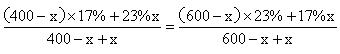
解出x,带入到方程的任何一边,可以求出现在两杯的浓度。
但是,解方程的过程是非常麻烦的,在行测考试当中我们缺的就是时间,所以要快速准确解出答案,我们可以采用
十字交叉法:
17% 2.4 400 2
X :
23% 3.6 600 3
左面列纵向做差,23-17=6,把6按照2:3来分,分成1.4和4.4,则求出x=20.6%。
如果我们对混合本质理解的深刻,可以用
分析法:
题中说从甲乙杯中取出相同的溶液,交叉导入另一杯中,则甲乙杯的溶液质量不变。而且后两杯溶液浓度相等。所以题干的过程我们可以转化为:把甲乙杯中的溶液先倒入一个大杯中,混合均匀后,再倒入甲杯400克,乙杯600克。则
后两杯的浓度为
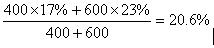
可见,对题目和方法理解的不同,则计算的速度也会不同。
我们再来看一道例题:
现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液。若从甲中取2100克,乙中取700克混合而成的消毒溶液的浓度为3%;若从甲中取900克,乙中取2700克,则混合而成的消毒溶液的浓度为5%。则甲、乙两种消毒溶液的浓度分别为:
A.3% 6% B.3% 4% C.2% 6% D.4% 6%
首先可以根据溶质相等,构造方程。
方程法:
设甲、乙溶液的浓度分别为x、y。则,
2100x+700y=3%*(2100+700)
900x+2700y=5%*(900+700)
解二元一次方程组可以得到答案。但是可以看出解方程组比较麻烦,会用很多的时间。所以我们应该寻找更为简便的做法。
分析猜答案法:
题目中说一定量的甲溶液和一定量的乙溶液混合,得到3%的溶液,则可以说明,甲乙溶液浓度一种大于3%,一种小于3%,同理可得,甲乙溶液浓度一种大于5%,一种小于5%。综合得出甲乙溶液,一种大于5%,一种小于3%。从选项看出,答案为C。
对题目的简单分析,我们不需要计算便可以快速得到答案,这就是我们所追求的,也是命题专家想让我们运用的方法。
经过上面的讲解,我们已经基本掌握了解决浓度问题的思路与方法,我们一起做一道练习。
甲,乙两种含金样品熔成合金,如甲的重量是乙的一半,得到含金68%的合金;如甲的重量是乙的3.5倍,得到含金(62 )%的合金。则乙的含金百分数为多少?
A.72% B.64% C.60% D.56%
我们采用分析猜答案法:
据题中如甲的重量是乙的一半,得到含金68%的合金;如甲的重量是乙的3.5倍,得到含金(62 )%的合金。可以看出,乙的重量所占比例要是高,则合金的含金量高,乙的重量所占比例低,则合金的含金量低,由此可以判断出,乙的含金量大于甲的含金量。
又因为,有一块合金的含金量为68%,所以必定甲乙一个大于68%,一个小于68%。根据上一段的结论,则推出,乙的含金量一定大于68%,则只有A答案。
在复习备考的过程中,我们要多思考、多积累,不要仅局限在做出一道题目,而应该把一道题做成三道题,经过一些练习,相信大家不在惧怕混合问题。
【运算中的混合问题】相关文章:
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题
★ 运算中的混合问题