随着时间的推移,2017全国各地省考也要开始了,各位备考的考生们也一定在努力的复习,这里查字典公务员教育专家就从一道2014年考察过的一道非常有趣的题目来给大家讲解下这类题型的解题思路,我们先来看这道题目。
右图小空格中已填上了1及7两个自然数,如果其他空格也填上相应不同的数,使得任意一个横行、任意一个纵列以及任意一条对角线上的3个数之和都等于111 。请问,位于中间的小正方形里应填的数是:( )。
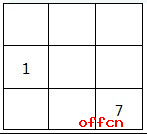
A.61 B.53
C.41 D.37
看到这里很多小伙伴都在思索这个题的解题思路了,我们先用常规方法来尝试着解决一下这个题目。我们可以代入选项进行排除,只有中间的小正方形为37时,才可满足题干条件。当中间5号位为37时,6号位即为:111-1-37=73;则3号位为:111-7-73=31;则7号位为:111-31-37=43;1号位为:111-1-43=67;2号位为:111-67-31=13;8号位为:111-13-37=61;各个数字各不相同,符合条件,故正确答案为D。
我们发现这类方法比较麻烦,其实这类题型属于幻方, 在33(三行三列)的正方形方格中,既不重复又不遗漏地填上1~9这9个连续的自然数,使每行、每列、每条对角线上的三个自然数的和均相等,通常这样的图形叫做三阶幻方。如果是在44(四行四列)的方格中进行填数,就要不重不漏地在44方格中填上16个连续的自然数,并且使方格的每行、每列及每条对角线上的四个自然数之和均相等,这样填出的图形就叫做四阶幻方。
幻方实际上就是一种填数游戏,它不仅限于三阶、四阶,还有五阶,六阶,,直到任意阶。
一般地,在nn(n行n列)的方格里,既不重复也不遗漏地填上nn个连续的自然数(注意,这nn个连续自然数不一定非要从1开始),每个数占1格,并使排在每一行、每一列以及每条对角线上的n个自然数的和都相等,我们把这个相等的和叫做幻和,n叫做阶,这样排成的数的图形叫做n阶幻方。
回到我们刚才所说的题上面的三阶幻方中,111是这个幻方的和,简称幻和. 所求是幻方最中心的数字,简称中心数。
三阶幻方的规律:
(1)幻和= 九个数之和
(2)中间数=幻和3
我们可以通过公式直接求得答案D,大家一定要掌握好!
【2017省考行测:走进你不知道的幻方】相关文章: